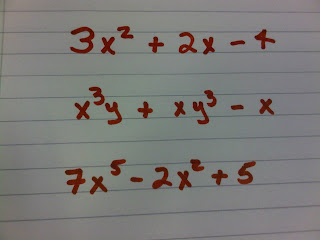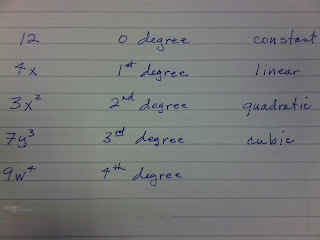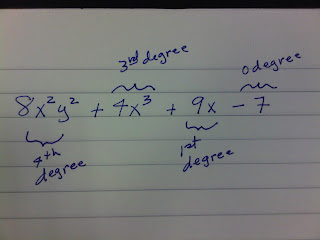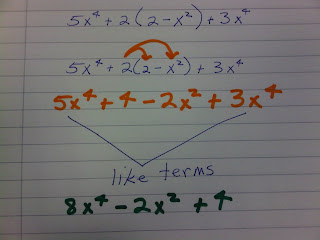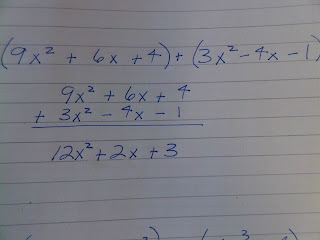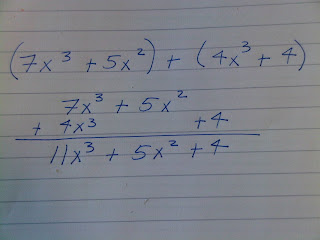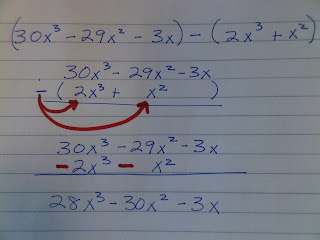Factoring Trinomials

In the last few blogs we have talked about multiplying binomials to produce a trinomial.

Now we are going to practice undoing or FACTORING trinomials.

We begin by listing all the factors of the constant term (term with no variable).

We look at the factors and see if any of them will add up to the middle term.










Last we look at the signs in the trinomial.  The last sign tells us whether the signs in the binomals are the same or different.  

The only way to multiply two numbers and get a positive number is for both numbers to be positive or both number are negative.

The sign for the middle term tells us if the signs in the binomials are poistive or negative.

When both signs in the trinomial are positive the signs in the parenthesis are positive.

(x + 3)(x + 10)

Mulitpying Special Binomials

When we multiply binomials there are times we run across special cases.

Most binomial multiplication looks like:

(x + 4)(x - 3)   or   (x - 2)(x - 7)    or   (x + 4)(x + 4)

When we multiply binomials with different constants (the number on the end without a variable), we end up with x squared, two like terms and a constant.

 We combine the like terms and end up with a trinomial written in standard form.



Squaring Binomials



When you square a binomial you must expand it to multiply each binomal using the FOIL method.









Difference of Two Squares

The difference of two squares is the product of the sum and difference of the same two terms and equals the difference of their squares.

Notice there is no middle term with the difference of two squares!

Even if we have more complicated binomials we still end up to the difference of perfect squares and no middle term.

FOIL Method

When we multiply binomials we use distribution. One way to remember the sequence for multiplying each term by each term is the FOIL method.


FOIL

F = first terms in each parenthesis

O = outer two terms in each parenthesis

I = inner two terms in the parenthesis

L = last two terms in the parenthesis











Combine like terms



Show your final answer

Polynomials

Nomial is another name for number or term. Poly means many. A polynomial is many numbers or many terms.

In algebra 1 we work with:

Monomials - - which means one term

Examples:

5
x
12y
-8xyz

Binomials - - which means two terms

Examples:

2x - 6
x + y
-8xyz + 12x

Notice that binomials are in lowest terms and have no like terms that can be combined.


Trinomials - - which means three terms

Examples:















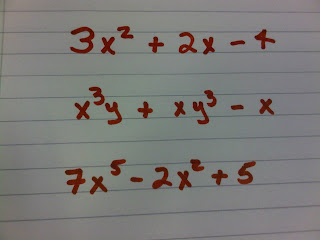
Each of these polynomials also has a DEGREE (or power). We find the degree by finding the highest power of each term. The term with the highest power sets the degree for the polynomial.


Polynomials can be:
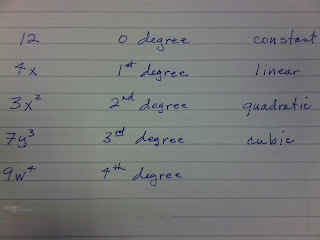
constant
(0 degree)

linear
(1st degree)

quadratic
(2nd degree)

cubic (3rd degree)

4th degree

5th degree

and on and on.






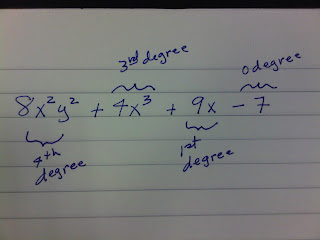
However, the highest degree of a polynomial is the combination of the powers in each individual term.








Standard Form of a Polynomial

As we have learned this year, there are specific ways to write algebraic terms. When writing polynomials we write them from the highest exponent to the lowest exponent.




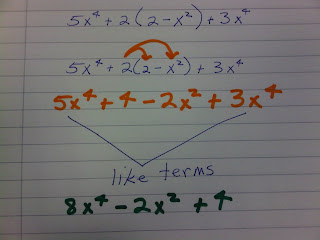
They are also written in reduced form so all mathematical process that can be done, must be done and all like-terms must be combined so the polynomial is in standard form.


Your final answer must be written in standard form, in lowest term.




Adding Polynomials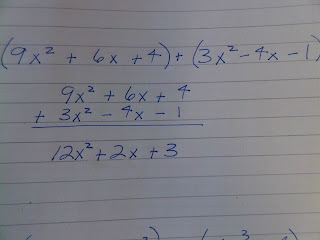



Adding vertically may be the easiest procedure:












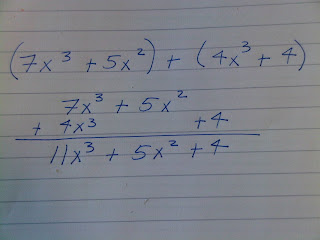
Remember to line up like terms so you are combining like variable with the same exponent.










Subtracting Polynomials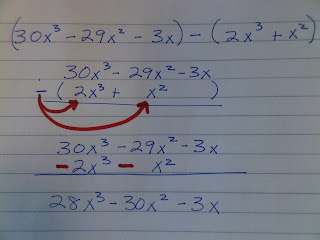


You must remember to distrbute the negative sign into the parentheses.

Graphing Exponential Functions

Graphing exponential functions can be as easy as graphing a linear function.


This is an exponential function. It is exponential because x is the exponent of 2.








To graph this equation you can make a t-table of values for x and calculate the value for y.













Then you graph the point for (x, y)


You will get half of a parabola.

Graphing Inequalities

We have already graphed inequalities on a number line but what is the procedure and outcome of graphing inequalities on a coordinate plane?

As with number line graphs, we need to simplify the inequality expression before we try to graph.


Therefor: 2y > 4x - 6 must be simplified in the same manner as an equaiton.

We need y to have a coefficient of 1 so would divide each term in the inequality by 2.

2y > 4x - 6
2


y > 2x - 3

We would then graph the inequality the same way we graph equations, beginning with the y-intercept (-3) and then using the slope to extend the line in two directions.

Negative Exponents

Negative exponents have nothing to do with negative numbers.

If we think of the use of negative exponents in Scientific Notation we can understand them a bit better.



A negative exponent with a power of 10 means it is a decimal.




10 to the -3 = 0.001, which we can also write as 1 over 1000.





When we use powers of 10 in Scientific Notation we are changing the negative power to a decimal and multiplying it by the significant digits.




Significant digits = 2.63

10 to -3 = 0.001

Multiply and you have 0.00263









A negative exponent means "the reciprocal"


2 to the -3 can be rewritten as 1 over 2 to the 3rd (or 2 cubed).

2 cubed is 8.

Our final answer is one over eight.





When we are simplifying a more complex problem that includes a negative exponent we:





reduce any fractions

combine the exponets for each base:

x
and
y

Finally put any negative exponents in the opposite area of the fraction:


If there is a negative in the numerartor -> put it in the denominator.

If there is a negative in the denominator -> put it in the numerator.

Your final answer should never include a negative exponent.

Graphing the Solution to Multiple Inequalities

In an earlier chapter we learned how to graph an inequality on a number line. Now we look at graphing inequalties on the coordinate plane.

To graph an inequalitiy we will use the same procedure as graphing an equation.

Simplify the inequality first then use the slope and intercept to graph.

2y > 4x - 6


2y > 4x - 6
2

y > 2x - 3

We anchor our line with the y-intercept and use the slope to extend the line in both directions.

With inequalities we use two different forms of a line:

dash or broken line for greater than or less than
or
solid line for great than or equal to or less than or equal to

But with inequalities we also shade in the section of the coordinate plane that includes all the possible values for y

If y is greater than 2x - 3 we shade in above the line.

For y is less than -x + 4 we shade below the line.

When we graph two inequalities we shade each individually and the area where they overlap is the solution to both inequalities

Important steps: simplify the inequality, graph the line using y-intercept and slope with either a dashed or solid line, shade above for greater and below for less.

Writing Equations for Word Problems

Sometimes figuring out how to write an equation for solving a word problems is the hardest part of the solution.

Here are some examples of word problems and the equations they lead to:

The sum of two numbers is 90. The difference between them is 75.
Find the two numbers.

Let a and b stand for the two numbers.

What do you know?

You are adding and subtracting the same two numbers.

Can you write one equations using addition and one using subtraction?

(Sum) = a + b = 90

(Difference) = a - b = 75

You could solve these equations using substitution or elimination.



A wildlife management station cares for sick birds and deer. The animals being cared for have a total of 25 heads and 74 feet (no heads or feet are missing!). How many of each animal are there?

Let b = birds and d = deer

What do we know?

If there are 25 heads, there must be a total of 25 animals

b + d = 25


What else do we know? Birds have two feet each and deer have four feet each and all the feet total 74.

2b + 4d = 74

Now we could solve by either substitution or elimination.


Breakfast: If two eggs with bacon cost £2.70 and one egg with bacon costs £1.80, what does bacon cost alone?

What do we know?

If we use e for eggs and b for bacon, we can write equations for each meal:

two eggs and bacon costs 2.70

2e + b = 2.7

one egg with bacon costs 1.80

e + b = 1.8

We can use substitution or elimination to solve these equation.

Walter is riding his bike to Thames City which is 28 miles away. It takes him one hour to make the ride against a head wind but it only takes him 48 minutes to return to St. John's Wood with a tail wind.

How fast was he riding without the wind and how strong was the wind?

If a is his average speed and w is the speed of the wind..... what else do we know?

(a - w) would be his speed (rate) riding against the wind.

(a + w) would be his speed (rate) riding with the wind

The distance for both parts of the trip is 28 miles.

It took one hour on the ride against the wind and 48 minutes (48/60 = 4/5 hour) to ride with the wind.

Using d = rt

28 = (a - w)1 (against the wind)

28 = (a + w)(4/5) (with the wind)

Simplify:

(1)28 = (a - w)1

28 = a - w

(5/4)28 = (a + w)(4/5)(5/4)

75 = a + w

We could then use substitution or elimination to solve the problem.

Stephanie received the results of her ERB scores in math and reading. Her reading score is 70 points less than her math score. Her total for the two parts is 1250.

Let m = math score and r = reading score.

What do we know?

Her math score plus her reading score is 1250.

m + r = 1250

What else do we know?

Her reading score is 70 points less than her math score.

r = m - 70

We could use substitution or elimination to solve this problem.

Simultaneous Equations

Simultaneous equations - two or more equations that have one or more points (solutions) in common.


There are three ways to solve simultaneous equations: graphing, substitution and elimination.

Graphing:

To solve for a common solution to two equations using graphing, you graph each line either on paper or on a graphing calculator.

The point at which they intersect is the solution to both equations.

Example: Graph the solution for y = x + 1 and y = (-1/2)x + 4


The solution is the point at which the lines cross.


Some lines have more than one solution.

y = 2x - 2 and 3y = 6x - 6

Lines with the same slope and same y-intercept will be graphed one on top of the other so that all points coincide. All points on the lines are solutions (infinite solutions).



Lines with the same slope but different y-intercepts are parallel and have no points in common. In this situation there is no solution.


Substitution:

To use substitution you must have at least one equation in simplest form that is equal to one of the variables.

Example:
x + 2y = 8 and y = x + 1

Since the second equation is in simplest form (y =), we will use it to substitute.

If y = x + 1 we can substitute the value for y into the other equation:

x + 2(x + 1) = 8

Simplify using distribution:

x + 2x + 2 = 8

Combine like terms:

3x + 2 = 8

Simplify:

3x + 2 - 2 = 8 - 2

3x = 6

Divide both sides by 3.

x = 2

Now we need to solve for y too!

Use either of the original equations: x + 2y= 8 and y = x + 1

y = 2 + 1

y = 3

The solutions to this system of equations is ( 2, 3)




Elimination:

In this form we will eliminate one of the variable to solve for one at a time, similar to substitution but using addition and subtraction.

We will start with the same equations we used in the first two forms but written in Standard Form:

y = x + 1 becomes -x + y = 1

y = -1/2x +4 becomes 2y = -x = 8 when we clear the fraction,

then x + 2y = 8 in Standard Form.

Line the two equations up so that like terms are in a column:

-x + y = 1
x + 2y = 8

Combine like terms vertically.

-x and x cancel each other out eliminating x from the equation.

y + 2y = 3y

1 + 8 = 9

3y = 9

y = 3

Substitute the value for y back into either original equations:

-x + y = 1 or x + 2y = 8

x + 2(3) = 8

x + 6 = 8

x + 6 - 6 = 8 - 6

x = 2

The solution for these two equations is (2, 3).



For more complicated equations we may need to multiply one of the equations to make the coefficient inverse.

2x + 3y = 11
2x + y = 3

We can eliminate the x by multiplying the second equation by -1

2x + 3y = 11
-2x - y = - 3

The x is eliminated leaving:

3y = 11
- y = - 3

Combining those terms gives us

2y = 8

y = 4

Substituting y back in either of the original equations:

2x + 3(4) = 11

2x + 12 = 11

2x + 12 - 12 = 11 - 12

2x = -1

x = - 1/2

Solution (-1/2, 4)


Some equations are even more complicated and you must multiply to get one variable ready for elimination.

2x + 3y = 7
3x - y = 5

Multiply the second equation by 3 to eliminate the y.

2x + 3y = 7
9x -3y = 15

y is eliminated leaving

11x = 22

x = 2

Solve for y.

2(2) + 3y = 7

4 + 3y = 7

4 - 4 + 3y = 7 - 4

3y = 3

y = 1

Solution (2, 1)


For even more complicated equations you may need to multiply both equations.
5x + 2y = 1
2x - 3y = -11

We can multiply the first equation by 2 and the second equation by -5.

2(5x + 2y = 1)
-5(2x - 3y = -11)

10x + 4y = 2
-10x + 15y = 55

The x is eliminated leaving:

4y = 2
15y = 55

19y = 57

divide by 19

y = 3

Substitute the value for y back in either original equation.

5x + 2y = 1

5x + 2(3) = 1

5x + 6 = 1

5x + 6 - 6 = 1 - 6

5x = -5

x = -1

Solution (-1, 3)

Solving Inequalities

In Lessons 4-2, 4-3 and 4-4 we have learned about graphing inequalities, solving when addition and subtraction are involved, solving when multiplication is involved and when there is a mix of operations on one or both sides of the inequality sign.

We always want to get our final answer simplified into the form of:

x > 3

When we are solving for a variable we work backwards through the order of operations:

Subtraction or Addition first

Division or Multiplication second

Clear any addition or subtraction first.

X + 4 < 12

subtract 4 from both sides

X + 4 - 4 < 12 - 4


X < 8


Clear any multiplication or division.


3x > 21


Multiply by the reciprocal

1/3 • 3x > 21 • 1/3


x > 7


For more complex problems such as

2(x - 3) < 4(x - 5)

Use the distributive property to clear the parenthesis first.

2x - 6 < 4x - 20

Then combine like terms by moving the terms with the variable to one side of the inequality and the terms without the variable to the other.

2x - 2x - 6 < 4x - 2x - 20

-6 < 2x - 20



-6 + 20 < 2x - 20 + 20

14 < 2x

Then multiply by the reciprocal.

1/2 • 14 < 2x • 1/2

7 < x or x > 7


Remember to always simplify each side of the inequality before you begin combining like terms.

Graphing Inequalities on a Number Line

When graphing inequalities on a number line there are conventions for the direction of the line and the end point of the line.

The end point is closed (filled in) when the symbols are

≤ less than or equal to
or
≥ greater than or equal

The end point is open when the symbols are

< less than
or
> greater than

The direction of the line on the graph is determined by whether the amount is greater than (going to the right on the number line) or less than (going to the left on the number line).

If the inequality is written with the variable on the left then the inequality symbol points in the direction of the line.

Semester Exam

Congratulations to everyone for studying very diligently for the semester exam. We had our usual assortment of grades: A's, B's C's and for the first time this year, grades lower than C.

I know some of you are disappointed with your results and I have options for you that may help. They will not help change your grade for this semester but they might help you do better in the second semester. Remember you need at 85% for the year to move on to geometry in grade 9.

This blog is one of the things I am going to try to see if it helps you improve not just your grade but your UNDERSTANDING of the algebra concepts. I am not interested in your grade - although you and your parents may be. I am interested in you understanding our algebra concepts SO WELL that you can use them to work any problem.

Toward that end, I will be blogging about our math lessons and send you a link so you can read and think about the concepts.

I hope this is one more thing that will make a difference in your understanding of algebra!